Réseau de neurones¶
Les réseaux de neurones, structures artificielles de neurones, constituent une approche permettant d’aborder sous des angles nouveaux les problèmes de perception, de mémoire, d’apprentissage et de raisonnement. Ils s’avèrent également des alternatives très prometteuses pour contourner certaines des limitations des ordinateurs classiques. De par leurs mécanismes inspirés de vraies cellules nerveuses (neurones) et leur traitement en parallèle de l’information, ils infèrent des propriétés nouvelles permettant de solutionner des problèmes jadis qualifiés de complexes.
Haykin en donne la définition suivante :
Un réseau de neurones est un processus distribué de manière massivement parallèle, qui a une propension naturelle à mémoriser des connaissances de façon expérimentale et de les rendre disponibles pour utilisation.
Il ressemble au cerveau en deux points :
- La connaissance est acquise au travers d’un processus d’apprentissage ;
- Les poids des connexions entre les neurones sont utilisés pour mémoriser la connaissance.
Modèle de neurone et réseau¶
Modèle d’un neurone¶
Le modèle mathématique d’un neurone artificiel est illustré à la figure 3.1. Un neurone est essentiellement constitué d’un intégrateur qui effectue la somme pondérée de ses entrées. Le résultat $n$ de cette somme est alors transformé par une fonction de transfert $f$ qui produit la sortie $y$ du neurone. Dès lors la sortie de l’intégrateur est donné par l’équation suivante :
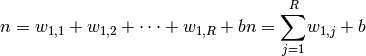
Cette sortie correspond à une somme pondérée des entrées plus ce que l’on nomme
le biais $b$ du neurone. De plus ce résultat s’appelle le niveau d’activation
du neurone et le biais $b$ est aussi dénommé le seuil d’activation du neurone.
Dès lors lorsque le niveau d’activation $n$ atteint ou dépasse le seuil $b$,
l’argument de 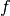 devient positif ou nul. Sinon il est négatif.
devient positif ou nul. Sinon il est négatif.
Ceci amène alors à considérer une représentation matricielle du neurone
(illustré à la figure 1.2). On remplace l’ensemble des poids par une matrice
ligne 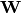 de dimension
de dimension 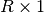 . L’équation de sortie
du neurone est alors donnée par :
. L’équation de sortie
du neurone est alors donnée par :
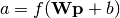
Cette équation permet alors d’introduire un modèle plus compact concernant le
neurone par rapport au schéma précédent. On représente les  entrées du
neurone par un rectangle noir, d’où sort la matrice colonne
entrées du
neurone par un rectangle noir, d’où sort la matrice colonne  de dimension
de dimension 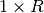 . Cette matrice est alors multipliée par la
matrice
. Cette matrice est alors multipliée par la
matrice 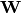 , ce qui permet d’obtenir un scalaire, correspondant
au niveau d’activation du neurone qui est alors comparé au biais
, ce qui permet d’obtenir un scalaire, correspondant
au niveau d’activation du neurone qui est alors comparé au biais 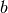 (également un scalaire). Enfin, la sortie du neurone est calculée par la
fonction d’activation $f$ et correspond toujours à un scalaire.
(également un scalaire). Enfin, la sortie du neurone est calculée par la
fonction d’activation $f$ et correspond toujours à un scalaire.
Fonction de transfert¶
La fonction d’activation, encore dénommée fonction de seuillage ou de transfert, sert à introduire une non-linéarité dans le fonctionnement du neurone. Celle-ci présente généralement trois intervalles distincts :
- En dessous du seuil, le neurone est considéré comme non-actif (selon les fonctions d’activation cette valeur peut valeur 0 ou -1, mais dans les deux cas elle s’apparente à un faux)
- Aux alentours du seuil, ce qui correspond à une phase de transition
- Au dessus du seuil, le neurone est considéré comme actif (lorsque la valeur de sortie tend vers 1 (valeur la plus généralement utilisée) on considère la sortie comme un vrai)
Architecture de réseau¶
Un réseau de neurones est un maillage de plusieurs neurones organisés en
couches. La construction d’une couche de 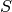 neurones se fait simplement
par assemblage des neurones entre eux. Les S neurones d’une même couches sont
tous reliés aux
neurones se fait simplement
par assemblage des neurones entre eux. Les S neurones d’une même couches sont
tous reliés aux 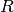 entrées. La couche est alors dite totalement
connectée. Dès lors,
entrées. La couche est alors dite totalement
connectée. Dès lors, 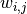 désigne les poids de la connexion reliant
le neurone
désigne les poids de la connexion reliant
le neurone 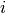 au neurone
au neurone 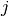 . L’ensemble des poids forme alors une
matrice
. L’ensemble des poids forme alors une
matrice 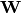 de dimension
de dimension 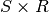 (
( étant
très souvent différent de
étant
très souvent différent de  ).
).
Finalement il ne reste plus qu’à connecter plusieurs couches entre elles pour
former le réseau. Chaque couche possède alors sa propre matrice de poids
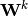 ,
, 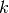 désignant le numéro de la couche.
désignant le numéro de la couche.
La dernière couche du réseau est dénommée “couche de sortie” et les autres couches “couches cachées”.
Perceptron multicouche¶
Le perceptron multicouche est un réseau orienté de neurones artificiels organisé en couches où l’information se propage dans un seul sens, de la couche d’entrée vers la couche de sortie. La couche d’entrée correspond à une couche virtuelle associée aux entrées du réseau et ne contient dès lors aucun neurone. Les couches suivantes sont des couches de neurones et les sorties de la dernière couche correspondent toujours aux sorties du réseau. De manière générale un perceptron multicouche peut posséder un nombre quelconque de couches et de neurones par couches (ou entrées).
Les neurones sont reliés entre eux à l’aide de connexions pondérées dont les poids gouvernent le fonctionnement du réseau et permettent de programmer une application de l’espace des entrées vers l’espace des sorties à l’aide d’une transformation non linéaire. La mise en place d’un perceptron multicouche dans l’optique de la résolution d’un problème donné passe par l’inférence de la meilleure application possible telle que définie par un ensemble de données d’apprentissage modélisées par des paires de vecteurs d’entrée et de sortie désirée. Cette inférence peut être réalisée grâce à la mise en place d’un algorithme de rétro-propagation d’erreurs.
Algorithme de rétro-propagation¶
Soit le couple 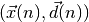 désignant la n^e donnée d’entraînement du réseau où :
désignant la n^e donnée d’entraînement du réseau où :
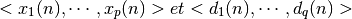
correspondent respectivement aux 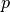 entrées et aux
entrées et aux 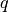 sorties
désirées du réseau. L’algorithme de rétro-propagation consiste donc à mesurer
l’erreur entre les sorties désirées
sorties
désirées du réseau. L’algorithme de rétro-propagation consiste donc à mesurer
l’erreur entre les sorties désirées 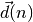 et les sorties obtenues
et les sorties obtenues
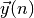 :
:
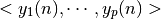
résultant de la propagation des entrées 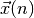 , et à rétro-propager
l’erreur au travers des couches précédentes.
, et à rétro-propager
l’erreur au travers des couches précédentes.
Règle du delta généralisée¶
D’après l’introduction sur les réseaux de neurones proposée précédemment, la sortie 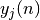 d’un neurone
d’un neurone 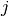 pour la donné d’entraînement
pour la donné d’entraînement 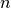 est définie par:
est définie par:
![y_{j} = f[v_{j}(n)] = f[\displaystyle{\sum_{i = 0}^{r}} w_{j,i}(n)y_{i}(n)](_images/math/ef75e770f70c19e3d520781120efef2bcd2d3497.png)
où 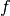 correspond à la fonction d’activation du neurone,
correspond à la fonction d’activation du neurone, 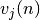 est la somme pondérée des entrées du neurone
est la somme pondérée des entrées du neurone 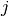 ,
, 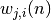 est
le poids de la connexion entre le neurone
est
le poids de la connexion entre le neurone 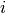 de la couche précédente et
le neurone
de la couche précédente et
le neurone 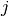 de la couche courante, et
de la couche courante, et 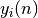 est la sortie
du neurone
est la sortie
du neurone 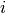 . On suppose ici que la couche précédente présente
. On suppose ici que la couche précédente présente
 neurones numérotés de 1 à
neurones numérotés de 1 à  , que le poids
, que le poids 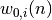 correspond au biais du neurones
correspond au biais du neurones 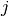 et que l’entrée
et que l’entrée 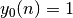 .
.
Afin de pouvoir démontrer la règle du “delta” généralisée on pose :
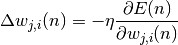
où 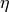 correspond au taux d’apprentissage ou gain de l’algorithme,
avec
correspond au taux d’apprentissage ou gain de l’algorithme,
avec 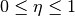 .
.
Soit 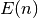 la somme des erreurs quadratiques observées sur l’ensemble
la somme des erreurs quadratiques observées sur l’ensemble
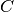 des neurones de la couche de sortie :
des neurones de la couche de sortie :
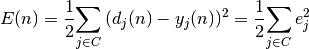
où 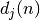 correspond à la sortie désirée du neurone
correspond à la sortie désirée du neurone 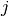 et
et
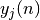 la sortie observée.
la sortie observée.
Par le chaînage des dérivées partielles, selon lequel 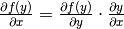 , on peut écrire :
, on peut écrire :
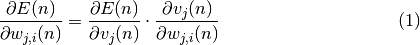
De par l’équation on observe que :
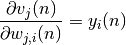
En effet on a :
![\frac{\partial v_{j}(n)}{\partial w_{j,i}(n)} = \frac{\partial [\displaystyle{\sum_{l = 0}^{r}} w_{j,l}(n)y_{l}(n)]}{\partial w_{j,i}(n)} = \frac{\partial [w_{j,i}(n)y_{i}(n)]}{\partial w_{j,i}} = y_{i}(n)](_images/math/3ccefbf87d8d8245b5255a46a455ef26e68a4a9d.png)
On définit alors :
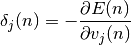
On sera en présence d’une règle de mise à jour des poids équivalente à la règle du “delta”, résultant d’une descente du gradient de l’erreur totale si l’on réalise la modification des poids comme suit :

Il convient dès lors de savoir ce que doit valoir 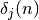 pour
chaque neurone
pour
chaque neurone 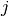 du réseau. Pour calculer
du réseau. Pour calculer 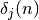 on
applique à nouveau un chaînage de dérivées partielles. On exprime alors
on
applique à nouveau un chaînage de dérivées partielles. On exprime alors
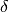 en tant que produit de deux facteurs, un premier facteur
reflétant le changement dans l’erreur en fonction de la sortie du neurone et un
second facteur représentant le changement de la sortie en fonction du
changement de l’entrée du neurone. Dès lors on a :
en tant que produit de deux facteurs, un premier facteur
reflétant le changement dans l’erreur en fonction de la sortie du neurone et un
second facteur représentant le changement de la sortie en fonction du
changement de l’entrée du neurone. Dès lors on a :
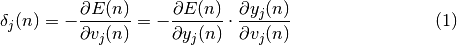
En calculant le second facteur on observe, de par l’équation 1, que :
![\begin{eqnarray}
\frac{\partial y_{j}(n)}{\partial v_{j}(n)} = f'[v_{j}(n)]
\end{eqnarray}](_images/math/299a995e1635c2e76023184ac147c8242f782973.png)
ce qui correspond tout simplement à la dérivée de la fonction d’activation du neurone  , évaluée au point
, évaluée au point  .
.
Afin de calculer le premier facteur de l’équation $(3.8)$, il est nécessaire de
considérer deux cas. Dans un premier temps considérons que le neurone $j$ soit
un neurone situé sur la couche de sortie du réseau. On pose  Dès lors on
a tout simplement :
Dès lors on
a tout simplement :
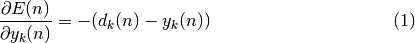
D’où, en modifiant l’équation (1.8) à l’aide de l’équation (1.9) et l’équation (1.10), on obtient :
![\begin{eqnarray}
\delta_{k}(n) = (d_{k}(n) - y_{k}(n))f'[v_{k}(n)]
\end{eqnarray}](_images/math/122ea14fcc76a9049b2bcdfd3fb438f76be58d25.png)
pour tout neurone  de la couche de sortie.
de la couche de sortie.
D’autre part, si  n’est pas la couche de sortie mais une couche cachée
n’est pas la couche de sortie mais une couche cachée
 , alors on ne sait pas quelle est la contribution du neurone h à
l’erreur observée en sortie du réseau. Cependant l’erreur peut être écrite en
fonction des
, alors on ne sait pas quelle est la contribution du neurone h à
l’erreur observée en sortie du réseau. Cependant l’erreur peut être écrite en
fonction des 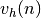 , i.e
, i.e 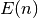
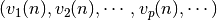 .
.
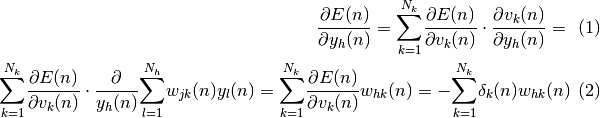
D’où par substitution on a :
![\begin{eqnarray}
\delta_{h}(n) = f'[v_{h}(n)]\displaystyle{\sum_{k = 1}^{N_{k}}}\delta_{k}(n)w_{hk}(n)
\end{eqnarray}](_images/math/de5c82f0b61212390bc2166c3e35932af0179088.png)
Les équations (3.11) et (3.14) donnent une procédure récursive permettant de
calculer 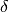 pour l’ensemble des neurones de toutes les couches du
réseau. La modification peut alors être réalisée grâce à l’équation (3.7).
pour l’ensemble des neurones de toutes les couches du
réseau. La modification peut alors être réalisée grâce à l’équation (3.7).
Algorithme de Vogl¶
L’algorithme de rétro-propagation seul propose une convergence assez lente, notamment due au fait que le paramètre d’apprentissage soit une valeur très proche de 0. Afin d’optimiser la vitesse de convergence, l’algorithme de Vogl, introduit dans T.P.Vogl, J.K.Mangis, AK.Riegler, W.T.Zink and D.L.Alkon - Accelerating the Convergence of the Back-propagation Method, Biological Cybernetics - 1988, a été mis en place.
Cet algorithme permet d’augmenter la vitesse de convergence de manière
conséquente en modifiant progressivement, i.e à chaque apprentissage, le taux
d’apprentissage. En effet, en observant l’équation (3.7) on remarque que la
variation des poids sur chaque retro-propagation d’erreur est proportionnelle
au taux d’apprentissage 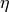 . Dès lors plus $eta$ augmente, plus la
vitesse de convergence augmente.
. Dès lors plus $eta$ augmente, plus la
vitesse de convergence augmente.
Cependant, la méthode du gradient, pour être stable, nécessite un taux d’apprentissage aussi petit que possible. Ainsi, dans l’optique de limiter et d’éviter au plus les oscillations, cet algorithme propose une évolution progressive du taux d’apprentissage, au fil de la convergence du réseau, ce qui, au final, augmente la vitesse de convergence et n’entraîne que peu d’oscillations.
L’algorithme de Vogl fait varier la taux d’apprentissage 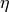 suite à chaque
apprentissage de la manière suivante :
suite à chaque
apprentissage de la manière suivante :
Si 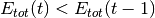 alors
alors 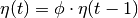
Si 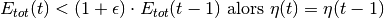
Si 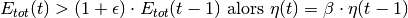
où 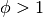 correspond au facteur d’accélération,
correspond au facteur d’accélération, 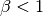 au facteur de décélaration,
au facteur de décélaration, 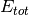 à la l’erreur totale et
à la l’erreur totale et 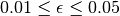 .
.
Quelques résultats¶
Voici quelques résultats obtenus pour le réseau de neurones avec l’algorithme de Vogl :
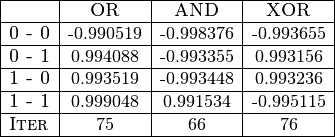
Reconnaissance de caractères¶
Introduction¶
Le cœur du logiciel reste la reconnaissance des caractères, ainsi une attention toute particulière doit être portée sur ce composant essentiel. Le principe général de la reconnaissance est le suivant : À partir d’une image d’un caractère sont extraites plusieurs caractéristiques uniques. Pour reconnaître le caractère en question, il faut comparer ces caractéristiques à celles trouvées pour des caractères fournis en apprentissage. La comparaison des caractéristiques du caractère voulu et des caractères appris permet de trouver le caractère à reconnaître.
Ce principe n’est que très général et est très variable en fonction des méthodes utilisées. En effet, deux étapes sont très importantes et à préciser : l’extraction des caractéristiques d’un caractère et la méthode de comparaison entre les caractéristiques des caractères appris et du caractère voulu.
Il existe plusieurs méthodes afin de trouver des caractéristiques d’un caractère. Le plus intuitive est la reconnaissance des formes et la description de celle-ci : par exemple un « P » est composée d’une barre verticale et d’une boucle accrochée à celle-ci en haut à droite. Cette méthode est la plus efficace puisqu’elle ne laisse presque pas de place au doute. Malheureusement cette méthode est très difficile à implanter car les caractéristiques ne sont pas uniformes d’un caractère à l’autre et la reconnaissance de formes n’est pas une chose aisée d’un point de vue algorithmique.
Une autre méthode beaucoup plus simple mais dont les résultats sont très variables et souvent assez peu satisfaisants est la méthode des bâtonnets. Elle consiste à poser des bâtonnets toujours de la même manière sur un caractère et de récupérer l’ensemble des bâtonnets coupés par les caractères, l’ensemble étant supposé unique pour chaque caractère différent. La comparaison est alors aisée puisqu’il ne s’agit que de vrai et de faux sur un certain nombre de bâtonnets.
Moments géométriques¶
D’une manière générale, les moments sont une suite de valeurs calculées par une
formule mathématique qui permettent de caractériser une image. Plus le nombre
de valeurs calculées augmente, plus la précision avec laquelle l’image est
décrite est grande. Plusieurs formules existent pour calculer des moments d’une
image. La plus simple et la plus basique est celle des moments cartésiens.
Notons 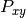 le pixel de l’image à la position
le pixel de l’image à la position 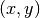 et
et
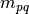 le moment cherché. La formule est la suivante :
le moment cherché. La formule est la suivante :
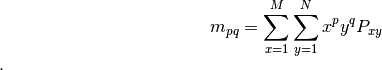
On obtient bien toute une famille de moments décrivant parfaitement l’image. Les moments cartésiens ont cependant deux inconvénients : Beaucoup d’informations sur les images sont redondantes, et une description précise de l’image nécessite beaucoup de calculs de moments. Le second problème est qui en fait en découle est que une grande différence d’une image sur l’autre peut-être répercutée sur seulement une petite différence sur les moments cartésiens. Ainsi une très grande précision sur le calcul des moments est nécessaire.
Ces deux problèmes sont résolus en utilisant une base de moments qui sont
orthogonaux. Deux fonctions 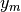 et
et 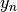 sont orthogonales si et
seulement si :
sont orthogonales si et
seulement si :
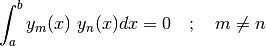
Il existe principalement deux bases orthogonales permettant de calculer les moments d’une images : il s’agit des bases de Legendre et de Zernike.
Moments de Zernike complexes¶
Les moments complexes de Zernike sont calculés sur une base de polynômes
complexes orthogonaux sur le cercle unitaire, i.e. 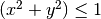 . Les moments complexes sont obtenus par la formule :
. Les moments complexes sont obtenus par la formule :
![\begin{displaymath} A_{mn} = \frac{m+1}{\pi} \sum_{x} \sum_{y} P_{xy}[V_{mn}(x,y)]^{*} ~~~~~\mbox{avec $x^{2} + y^{2} \leq ~1$} \end{displaymath}](_images/math/431d3aa9e4d0c1466caeb26b7bc98f491dc06da3.png)
avec 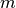 allant de
allant de 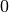 à
à 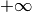 et où
et où  indique
le conjugué complexe. L’entier relatif $n$ est sujet à ces conditions :
indique
le conjugué complexe. L’entier relatif $n$ est sujet à ces conditions :
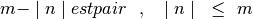
La base orthogonale utilisée pour le calcul des moments de Zernike sont les
polynômes complexes 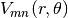 tels que :
tels que :
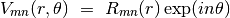
où 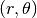 sont définis sur le cercle unitaire.
sont définis sur le cercle unitaire. 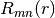 est le polynôme radial orthogonal défini par :
est le polynôme radial orthogonal défini par :
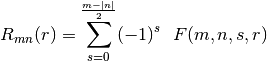
avec :
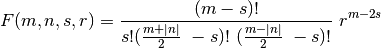
À partir de ces formules, il est possible de calculer tous les moments de Zernike, du moins jusqu’à l’ordre 12 car au-delà les factorielles dépassent les représentations des entiers en OCaml et les résultats sont faux. Cependant l’ordre 12 correspond à 47 moments différents, ce qui est suffisant pour caractériser correctement une image.
Les moments calculés sont des nombres complexes. Pour les utiliser correctement, il ne faut pas oublier de prendre leur module. Un des principaux avantages de l’utilisation des moments de Zernike est que ceux-ci sont par nature invariants par rotation et peuvent être rendus invariant au changement d’échelle.
Implantation des moments de Zernike¶
Une fois les formules mathématiques en main, il n’est pas très difficile d’implanter le calcul. Il suffit en effet de transformer les formules mathématiques en fonction OCaml. Cependant des soucis apparaissent à l’implantation des différentes formules. Le premier est le changement de coordonnées entre la matrice contenant les pixels de l’images (sous forme de coordonnées cartésiennes donc) et le repère de coordonnées polaires nécessaire pour calculer les polynômes de Zernike. Ce changement de repère induit une erreur dans le calcul des moments car les valeurs contenues dans la matrice des pixels de l’image sont de par leur formes sur des valeurs discrètes en x et en y. Ainsi le changement de coordonnées utilisé pour la somme appelle des pixels qui n’existent pas entre les pixels disponibles et une interpolation doit être faite. Le second problème est le choix de de la position du cercle unitaire
L’invariance à l’échelle est très importante car elle permet de reconnaître une image par ses caractéristiques fournies par Zernike quelque soit sa taille et ainsi un caractère est reconnu pour toutes les tailles de police de caractère. Cette invariance est de fait obtenue lors du choix du cercle unitaire qui est plus grand si l’image est plus grande et renvoie donc les mêmes résultats.